Lý thuyết
Đạo hàm của một hàm số là giới hạn của tỉ số sau:
![]()
Ví dụ: Đạo hàm của ![]() là
là ![]() .
.
📘 Một số công thức đạo hàm cơ bản
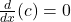 với
với  là hằng số
là hằng số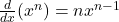
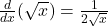
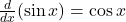
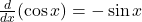
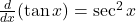
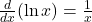
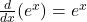
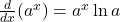 , với
, với 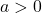
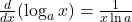 , với
, với 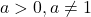
Bài tập trắc nghiệm
1. Đạo hàm của ![]() là:
là:
2. Đạo hàm của ![]() là:
là:
3. Đạo hàm của ![]() là:
là:
#Toánphổthông
